Top 11 ICO Volume Calculator Free online
Sphere Volume
Cube Volume
Cylinder Volume Calculator
Cone Volume
Rectangular Tank Volume
Capsule Volume (cylinder + two hemispheres)
Spherical Cap (STANDARD)
Conical Frustum Volume
Ellipsoid Volume
Square Pyramid Volume
Tube (hollow cylinder) Volume
ICO Volumetric Calculator
Volume calculation describes the total 3 dimensional space an object encloses or a container can hold. In scientific terms, the SI unit of volume is the cubic meter (m³). In everyday applications, volume often reflects capacity—how much liquid, sand, or concrete can be stored inside a container, truck, troley—rather than the physical space the container itself occupies.
Many common shapes follow direct mathematical formulas how to calculate for volume. Irregular shapes may be divided into simpler parts or modeled using an integral calculator volume when exact boundaries are known. For shapes without definable equations, engineers use numerical methods to approximate volume.
In situations where material density is constant and known, volume can also be derived from weight. This guide explains formulas for 11 Top commonly used geometrical shapes for example sphere, cube, tube, cylinderical, cone, recatangular, capsule, trustum, sq pyramids, spherical cap, and Ellipsoid.
Volume Calculator Sphere
A sphere is the 3-dimensional form of a perfect circle. Every point on its surface lies at the same distance (its radius, r) from the center. The longest possible line through the center is the diameter d. Balls, bubbles, and planets commonly approximate spherical geometry. The formula to estimate volume of a sphere is:
Formula Sphere Volume = 4/3 π r³
Example:
Joe plans to craft a crystal orb for her living room shelf. If the glass sphere has a radius of 0.25 ft, he calculates how much molten glass is needed:
Spherical Volume = 4/3 × π × (0.25)³ = 0.0654 ft³
Cone Volume Calculator
A cone narrows smoothly from a circular base to a single point known as the apex. Only right circular cones—those with height h perpendicular to the base—are considered here. The formula for volume of a cone estimator used is:
Cone Volume Formula = 1/3 π r² h

Example:
Tania wants to design a set of decorative incense cones. For one cone with radius 1.5 in and height 6 in:
Volume = 1/3 × π × (1.5)² × 6 = 14.137 in³
Cube Volume Calculator
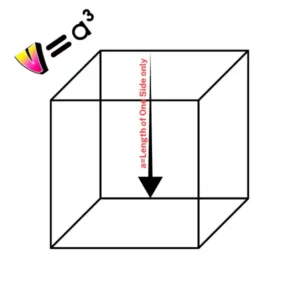
A cube is a special rectangular solid where all six faces are equal squares. Each edge measures the same length a. Its formula is one of the simplest:
Volume = a³
Example:
Khan stores his mineral samples in identical cubic boxes. Each cube has an edge length of 1.9 ft: Formula how to calculate volume of a cube is as follows
Applying in Formula for cube Volume = (1.9)³ = 6.859 ft³
Volume calculator Cylinder
A right cylinder features 2 circular bases aligned one above the other, wit h uniform radius r and height h. The volume of cylinder calculator formula is:
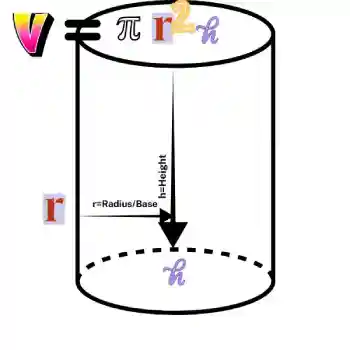
Volume = π r² h
Example:
Michael collects rainwater in a barrel with radius 2.9 ft and height 4 ft:
Volume = π × (2.9)² × 4 = 105.683 ft³
Rectangular Tanker Volume Calculator
A rectangular tanker resembles a stretched cube with different side lengths: length × width × height. To find volume rectangle, use formula as follows
formula = L × W × H
Mentioned formula is also comuting how to find volume of a rectangular prism, simply multiply its length, width, and height. This formula helps you measure volume of a rectangle, to calculate material capacity, or solve geometry problems with quick and accurate results.
Example:
Rehan keeps aquarium fish in a rectangular tank measuring 6 ft × 3 ft × 2 ft. He uses rectangle volume calculator and checks the result using formula as below.
Volume = 6 × 3 × 2 = 36 ft³
so the rectangular tank volume is 36 cube feet.
Capsule Volume Calculator
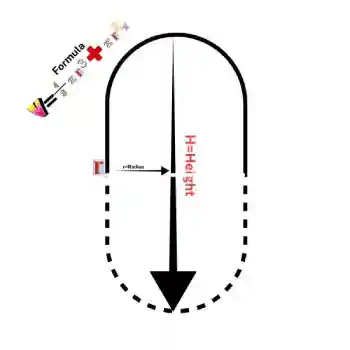
A capsule combines a cylinder with two hemispheres attached at both ends. Its formula combines the cylinder and sphere volumes:
Capsule Volume Formula= π r² h + 4/3 π r³
Example:
Sara designs a capsule-shaped float for a science project. With radius 0.9 ft and cylindrical height 2 ft:
Volume = π × (0.9)² × 2 + 4/3 × π × (0.9)³ = 8.113 ft³
Spherical Cap Volume calculator
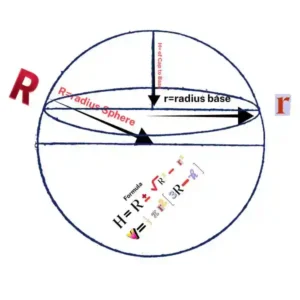
A spherical cap is created by slicing a sphere with a plane, leaving a curved top of height h and sphere radius R.
Volume = 1/3 π h² (3R − h)
Example:
Arham sands off the top of a wooden sphere to make a flat base. If R = 5 in and the removed cap height is 1 in:
Volume = 1/3 × π × (1)²(3 × 5 − 1) = 13.351 in³
Conical Frustum Volume Calculator
A frustum appears when a cone is cut by a plane parallel to its base, leaving two circular faces with radii r and R.
Volume = 1/3 π h (r² + rR + R²)
Example:
Kierra molds a decorative vase shaped like a conical frustum, with height 7 in, top radius 1 in, and bottom radius 3.5 in:
Volume = 1/3 × π × 7 (1² + 1×3.5 + 3.5²) = 106.814 in³
Ellipsoid
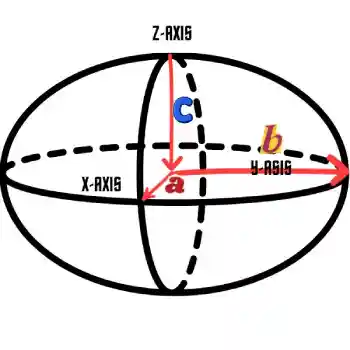
An ellipsoid stretches a sphere along its principal axes a, b, and c. The formula is:
Volume = 4/3 π a b c
Example:
Omar carves an ellipsoid sculpture with axes 2 in, 3 in, and 4 in:
Volume = 4/3 × π × 2 × 3 × 4 = 100.531 in³
Square Pyramid Volume calculator
A square pyramid has a square base with side a and height h measured perpendicular to the base.
Volume = 1/3 a² h
Example:
Lyla builds a model pyramid for school with base edge 6 ft and height 10 ft: To find volue of a pyramid, use formula as follow;
Pyramid Volume Equation: V = (1/3) × B × h
Where:
V = volume of the pyramid
B = area of the base h = height (perpendicular from base to apex
Putting value in Pyramid Volume Formula we get = 1/3 × 6² × 10 = 120 ft³
Tube (Hollow Cylinder) Volume Calculator
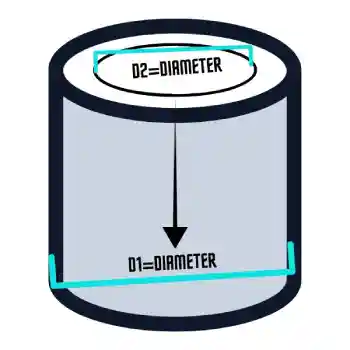
A tube is a cylinder with material thickness—defined by an outer diameter d₁, inner diameter d₂, and length l. The formula subtracts the inner cylinder from the outer:
Volume = π (d₁² − d₂²)/4 × l
Example:
Rohan constructs a handrail using metal tubing. For tubing with outer diameter 4 in, inner diameter 3.2 in, and length 60 in:
Volume = π × (4² − 3.2²)/4 × 60 = 251.327 in³
Bottom Line
The volume calculator helps you quickly determine the space any 3D shape occupies using accurate formulas and simple inputs. It is ideal for students, engineers, builders, and anyone working with measurements.
Do enter precise dimensions, follow unit consistency, and double-check values before calculating. Do use the tool for estimating capacity, designing projects, or learning geometry. Don’t mix unit systems, guess measurements, or rely on approximations for critical engineering work.
Don’t use the ICO volume calculator for irregular objects without proper data. This tool ensures accuracy, efficiency, and clarity for all volume-related tasks.
Why is it impossible to calculate the volume of a circle, and which circular-based 3D shapes actually allow proper volume calculation?
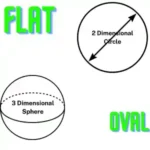
A circle lives entirely in a flat, 2-dimensional world—it stretches across length and width, but never rises into height. Because volume needs all three dimensions, a circle simply doesn’t qualify. It has area, not volume.
But the moment a circle steps into the 3D space, things change. Turn it into a sphere by rotating it, or extend it upward to form a cylinder, and suddenly volume becomes measurable. These 3D shapes—built from the circle—carry the formulas that let you compute how much space they occupy.
Can we find the radius based area of a sphere by sphere volume calculator, or is that impossible since spheres don’t have flat surfaces?
A sphere has no flat 2D surface, so calculating its “area” like a circle is impossible. But we can calculate its curved surface area and volume of sphere using: 𝓥 = ⁴⁄₃π𝓻³
Is it possible to calculate the area of a cube’s face by knowing only its total volume?
Not directly. A cube’s volume alone doesn’t reveal the face area unless you know the edge length.
Once the edge is known, the volume becomes: 𝓥 = 𝓼³
Can we find the volume of a box if only the diagonal is given?
Not from the diagonal alone. You need length, width, and height.
Then the correct volume is: 𝓥 = 𝓵 × 𝔀 × 𝓱
How to calculate volume of a cylinder using only its circumference?
No volume of cylinder can not be calculated using circumerence only because— circumference alone cannot reveal height.
But with radius and height, the volume is: 𝓥 = π𝓻²𝓱
Is it possible to calculate a cone’s volume using only its slant height?
Not possible. Slant height doesn’t tell us the radius or true height.
The valid formula is: 𝓥 = ¹⁄₃π𝓻²𝓱
Can the volume of a triangular prism be calculated from just one side of the triangle?
No — a single side gives incomplete information.
To calculate volume, you need triangle area and prism length: 𝓥 = (½𝓫𝓱) × 𝓵
Can you find the volume of a pyramid if only the slanted edges are known?
No — slanted edges don’t reveal base area or true height.
For correct volume we use: 𝓥 = ¹⁄₃(𝓑 × 𝓱)
Can an ellipsoid’s volume be calculated using just one radius?
Impossible — an ellipsoid stretches in three different directions.
Its volume requires all three radii: 𝓥 = ⁴⁄₃π𝓪𝓫𝓬
Can we figure out how much space a torus holds by knowing only the tube thickness?
No — the ring radius is also needed.
With both radii, the volume becomes: 𝓥 = 2π²𝓡𝓻²
Can we calculate a volume of capsule without knowing where the cylindrical part ends and the rounded part begins?
No — you must know the cylinder height and radius.
Then volume = cylinder + sphere parts:
𝓥 = π𝓻²𝓱 + ⁴⁄₃π𝓻³
Can we compute the volume of a hemisphere without first knowing the sphere it came from?
No — the hemisphere volume still depends entirely on the sphere’s radius.
Then the formula is: 𝓥 = ²⁄₃π𝓻³
How to calculate volume of a cube, without using Volume calculator
To calculate the volume of a cube, measure the length of any one side and multiply it by itself three times. Since all edges are equal, the formula becomes V = s³. This gives the total space the cube occupies in three dimensions.
Can we find volume of a cylinder with diameter only ?
No, you cannot find the volume of a cylinder with only the diameter. You also need the height (h)

